About the CoMSES Model Library more info
Our mission is to help computational modelers develop, document, and share their computational models in accordance with community standards and good open science and software engineering practices. Model authors can publish their model source code in the Computational Model Library with narrative documentation as well as metadata that supports open science and emerging norms that facilitate software citation, computational reproducibility / frictionless reuse, and interoperability. Model authors can also request private peer review of their computational models. Models that pass peer review receive a DOI once published.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and feel free to contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 22 results Python clear search
Structural Violence and Neurobiological Adaptation: Modeling the Trajectory of Youth Outside of Care
masterpiece33330-prog | Published Thursday, November 27, 2025This study presents a System Dynamics (SD) model that explores the “trajectories of homelessness” among youth outside of the formal care system. Unlike traditional approaches that view runaway behavior as a discrete choice, this model reinterprets it as a neurobiological adaptation to chronic resource deprivation and systemic neglect.
The model incorporates key mechanisms such as ‘Allostatic Load’ accumulation, ‘PFC-Amygdala Switching’, and the ‘Iatrogenic Effects’ of shelter policies. It utilizes Monte Carlo simulations to demonstrate how structural factors create a “probabilistic vulnerability,” trapping youth in cycles of survival crime and isolation regardless of individual resilience.
The uploaded code includes a Python implementation of the model to ensure reproducibility of the stochastic analysis presented in the paper.
Peer reviewed AgModel
Isaac Ullah | Published Friday, December 06, 2024AgModel is an agent-based model of the forager-farmer transition. The model consists of a single software agent that, conceptually, can be thought of as a single hunter-gather community (i.e., a co-residential group that shares in subsistence activities and decision making). The agent has several characteristics, including a population of human foragers, intrinsic birth and death rates, an annual total energy need, and an available amount of foraging labor. The model assumes a central-place foraging strategy in a fixed territory for a two-resource economy: cereal grains and prey animals. The territory has a fixed number of patches, and a starting number of prey. While the model is not spatially explicit, it does assume some spatiality of resources by including search times.
Demographic and environmental components of the simulation occur and are updated at an annual temporal resolution, but foraging decisions are “event” based so that many such decisions will be made in each year. Thus, each new year, the foraging agent must undertake a series of optimal foraging decisions based on its current knowledge of the availability of cereals and prey animals. Other resources are not accounted for in the model directly, but can be assumed for by adjusting the total number of required annual energy intake that the foraging agent uses to calculate its cereal and prey animal foraging decisions. The agent proceeds to balance the net benefits of the chance of finding, processing, and consuming a prey animal, versus that of finding a cereal patch, and processing and consuming that cereal. These decisions continue until the annual kcal target is reached (balanced on the current human population). If the agent consumes all available resources in a given year, it may “starve”. Starvation will affect birth and death rates, as will foraging success, and so the population will increase or decrease according to a probabilistic function (perturbed by some stochasticity) and the agent’s foraging success or failure. The agent is also constrained by labor caps, set by the modeler at model initialization. If the agent expends its yearly budget of person-hours for hunting or foraging, then the agent can no longer do those activities that year, and it may starve.
Foragers choose to either expend their annual labor budget either hunting prey animals or harvesting cereal patches. If the agent chooses to harvest prey animals, they will expend energy searching for and processing prey animals. prey animals search times are density dependent, and the number of prey animals per encounter and handling times can be altered in the model parameterization (e.g. to increase the payoff per encounter). Prey animal populations are also subject to intrinsic birth and death rates with the addition of additional deaths caused by human predation. A small amount of prey animals may “migrate” into the territory each year. This prevents prey animals populations from complete decimation, but also may be used to model increased distances of logistic mobility (or, perhaps, even residential mobility within a larger territory).
…
Agent-based model of power dynamics in agri-food systems
Tim Williams | Published Sunday, October 27, 2024 | Last modified Thursday, June 12, 2025This is a stylised agent-based model designed to explore the conditions that lead to lock-ins and transitions in agri-food systems.
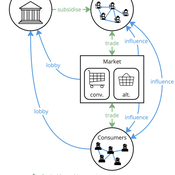
The model represents interactions between four different types of agents: farmers, consumers, markets, and the state. Farmers and consumers are heterogeneous, and at each time step decide whether to trade with one of two market agents: the conventional or alternative. The state agent provides subsidies to the farmers at each time step.
The key emergent outcome is the fraction of trade in each time step that flows through the alternative market agent. This arises from the distributed decisions of farmer and consumer agents. A “sustainability transition” is defined as a shift in the dominant practices (and associated balance of power) towards the alternative paradigm.
…
Integrate land use policies into the agent-based model to simulate land use change
Jing Gao | Published Sunday, June 09, 2024Detailed information will be presented after the journal paper is published.
Peer reviewed Agent-Based Ramsey growth model with endogenous technical progress (ABRam-T)
Sarah Wolf Aida Sarai Figueroa Alvarez Malika Tokpanova | Published Wednesday, February 14, 2024 | Last modified Monday, February 19, 2024The Agent-Based Ramsey growth model is designed to analyze and test a decentralized economy composed of utility maximizing agents, with a particular focus on understanding the growth dynamics of the system. We consider farms that adopt different investment strategies based on the information available to them. The model is built upon the well-known Ramsey growth model, with the introduction of endogenous technical progress through mechanisms of learning by doing and knowledge spillovers.
Peer reviewed Dynamic Equilibria Prediction: Experience-Weighted Attraction (EWA), Python Implementation
Vinicius Ferraz | Published Friday, December 02, 2022This project is based on a Jupyter Notebook that describes the stepwise implementation of the EWA model in bi-matrix ( 2×2 ) strategic-form games for the simulation of economic learning processes. The output is a dataset with the simulated values of Attractions, Experience, selected strategies, and payoffs gained for the desired number of rounds and periods. The notebook also includes exploratory data analysis over the simulated output based on equilibrium, strategy frequencies, and payoffs.
Cellular automata model of social networks
Rubens de Almeida Zimbres | Published Tuesday, August 02, 2022This project was developed during the Santa Fe course Introduction to Agent-Based Modeling 2022. The origin is a Cellular Automata (CA) model to simulate human interactions that happen in the real world, from Rubens and Oliveira (2009). These authors used a market research with real people in two different times: one at time zero and the second at time zero plus 4 months (longitudinal market research). They developed an agent-based model whose initial condition was inherited from the results of the first market research response values and evolve it to simulate human interactions with Agent-Based Modeling that led to the values of the second market research, without explicitly imposing rules. Then, compared results of the model with the second market research. The model reached 73.80% accuracy.
In the same way, this project is an Exploratory ABM project that models individuals in a closed society whose behavior depends upon the result of interaction with two neighbors within a radius of interaction, one on the relative “right” and other one on the relative “left”. According to the states (colors) of neighbors, a given cellular automata rule is applied, according to the value set in Chooser. Five states were used here and are defined as levels of quality perception, where red (states 0 and 1) means unhappy, state 3 is neutral and green (states 3 and 4) means happy.
There is also a message passing algorithm in the social network, to analyze the flow and spread of information among nodes. Both the cellular automaton and the message passing algorithms were developed using the Python extension. The model also uses extensions csv and arduino.
Peer reviewed Evolutionary Economic Learning Simulation: A Genetic Algorithm for Dynamic 2x2 Strategic-Form Games in Python
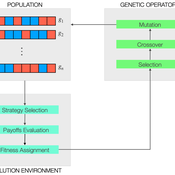
Vinicius Ferraz Thomas Pitz | Published Friday, April 08, 2022This project combines game theory and genetic algorithms in a simulation model for evolutionary learning and strategic behavior. It is often observed in the real world that strategic scenarios change over time, and deciding agents need to adapt to new information and environmental structures. Yet, game theory models often focus on static games, even for dynamic and temporal analyses. This simulation model introduces a heuristic procedure that enables these changes in strategic scenarios with Genetic Algorithms. Using normalized 2x2 strategic-form games as input, computational agents can interact and make decisions using three pre-defined decision rules: Nash Equilibrium, Hurwicz Rule, and Random. The games then are allowed to change over time as a function of the agent’s behavior through crossover and mutation. As a result, strategic behavior can be modeled in several simulated scenarios, and their impacts and outcomes can be analyzed, potentially transforming conflictual situations into harmony.
Correlated random walk
Thibault Fronville | Published Friday, April 01, 2022 | Last modified Monday, April 25, 2022The first simple movement models used unbiased and uncorrelated random walks (RW). In such models of movement, the direction of the movement is totally independent of the previous movement direction. In other words, at each time step the direction, in which an individual is moving is completely random. This process is referred to as a Brownian motion.
On the other hand, in correlated random walks (CRW) the choice of the movement directions depends on the direction of the previous movement. At each time step, the movement direction has a tendency to point in the same direction as the previous one. This movement model fits well observational movement data for many animal species.
The presented agent based model simulated the movement of the agents as a correlated random walk (CRW). The turning angle at each time step follows the Von Mises distribution with a ϰ of 10. The closer ϰ gets to zero, the closer the Von Mises distribution becomes uniform. The larger ϰ gets, the more the Von Mises distribution approaches a normal distribution concentrated around the mean (0°).
This model is implemented in python and can be used as a building block for more complex agent based models that would rely on describing the movement of individuals with CRW.
Pastoralscape
Matthew Sottile | Published Tuesday, October 12, 2021Pastoralscape is a model of human agents, lifestock health and contageous disease for studying the impact of human decision making in pastoral communities within East Africa on livestock populations. It implements an event-driven agent based model in Python 3.
Displaying 10 of 22 results Python clear search