About the CoMSES Model Library more info
Our mission is to help computational modelers at all levels engage in the establishment and adoption of community standards and good practices for developing and sharing computational models. Model authors can freely publish their model source code in the Computational Model Library alongside narrative documentation, open science metadata, and other emerging open science norms that facilitate software citation, reproducibility, interoperability, and reuse. Model authors can also request peer review of their computational models to receive a DOI.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with additional detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 183 results for "J Gary Polhill" clear search
Enhancing recycling of construction materials; an agent based model with empirically based decision parameters
Christof Knoeri Igor Nikolic Hans-Joerg Althaus Claudia Binder | Published Sunday, October 21, 2012 | Last modified Monday, June 09, 2014This model allows for analyzing the most efficient levers for enhancing the use of recycled construction materials, and the role of empirically based decision parameters.
Peer reviewed Multilevel Group Selection I
Garry Sotnik Thaddeus Shannon Wayne W. Wakeland | Published Tuesday, April 21, 2020 | Last modified Saturday, July 03, 2021New theoretical agent-based model of population-wide adoption of prosocial common-pool behavior with four parameters (initial percent of adopters, pressure to change behavior, synergy from behavior, and population density); dynamics in behavior, movement, freeriding, and group composition and size; and emergence of multilevel group selection. Theoretical analysis of model’s dynamics identified six regions in model’s parameter space, in which pressure-synergy combinations lead to different outcomes: extinction, persistence, and full adoption. Simulation results verified the theoretical analysis and demonstrated that increases in density reduce number of pressure-synergy combinations leading to population-wide adoption; initial percent of contributors affects underlying behavior and final outcomes, but not size of regions or transition zones between them; and random movement assists adoption of prosocial common-pool behavior.
MedLanD Modeling Laboratory
C Michael Barton Isaac Ullah Gary Mayer Sean Bergin Hessam Sarjoughian Helena Mitasova | Published Friday, May 08, 2015 | Last modified Thursday, December 14, 2017The MML is a hybrid modeling environment that couples an agent-based model of small-holder agropastoral households and a cellular landscape evolution model that simulates changes in erosion/deposition, soils, and vegetation.
PSMED - Patagonia Simple Model of Ethnic Differentiation
Joan A Barceló J A Cuesta Florencia Del Castillo Ricardo Del Olmo José M Galán Laura Mameli Francisco J Miguel David Poza José I Santos Xavier Vilà | Published Tuesday, December 10, 2013Patagonia PSMED is an agent-based model designed to study a simple case of Evolution of Ethnic Differentiation. It replicates how can hunter-gatherer societies evolve and built cultural identities as a consequence of the way they interacted.
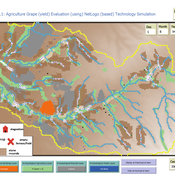
Peer reviewed Agriculture.Grape.yield.Evaluation.using.NetLogo.based.Technology.Simulation (AGENTS): A NetLogo agent-based model developed to assess viticulture efficiency in Byzantine Shivta.
Barak Garty Guy BarOz Gil Gambash Sharona T Levy | Published Friday, December 06, 2024AGENTS model is an agent-based computational framework designed to explore the socio-ecological and economic dynamics of agricultural production in the Byzantine Negev Highlands, with a focus on viticulture. It integrates historical, environmental, and social factors to simulate settlement sustainability, crop yields, and the impacts of varying climate conditions. The model is built in NetLogo and incorporates GIS-based topographical and hydrological data. Key features include the ability to assess climate impacts on crop profitability and settlement strategies, evaluate economic outputs of ancient vineyards, and simulate agent decision-making processes under diverse scenarios.
The AGENTS model is highly flexible, enabling users to simulate agricultural regimes with any two crops: one cash crop (a crop grown for profit, e.g., grapevines) and one staple crop (a crop grown for subsistence, e.g., wheat). While the default setup models viticulture and wheat cultivation in the Byzantine Negev Highlands, users can adapt the model to different environmental and socio-ecological contexts worldwide—both past and present.
Users can load external files to customize precipitation, evaporation, topography, and labor costs (measured as man-days per 0.1ha, converted to kg of wheat per model patch size area), and can also edit key parameters related to yield calculations. This includes modifying crop-specific yield formulas, soil and runoff indices, and any factors influencing crop performance. The model inherently simulates cash crops grown in floodplain regions and staple crops cultivated along riverbanks, providing a powerful tool to investigate societal resilience and responses to climate stressors across diverse environments.
…
WeDiG Sim
Reza Shamsaee | Published Monday, May 14, 2012 | Last modified Saturday, April 27, 2013WeDiG Sim- Weighted Directed Graph Simulator - is an open source application that serves to simulate complex systems. WeDiG Sim reflects the behaviors of those complex systems that put stress on scale-free, weightedness, and directedness. It has been implemented based on “WeDiG model” that is newly presented in this domain. The WeDiG model can be seen as a generalized version of “Barabási-Albert (BA) model”. WeDiG not only deals with weighed directed systems, but also it can handle the […]
Peer reviewed Price Evolution with Expectations
J M Applegate Gesine Steudel Armin Haas Carlo Jaeger | Published Friday, September 10, 2021The Price Evolution with Expectations model provides the opportunity to explore the question of non-equilibrium market dynamics, and how and under which conditions an economic system converges to the classically defined economic equilibrium. To accomplish this, we bring together two points of view of the economy; the classical perspective of general equilibrium theory and an evolutionary perspective, in which the current development of the economic system determines the possibilities for further evolution.
The Price Evolution with Expectations model consists of a representative firm producing no profit but producing a single good, which we call sugar, and a representative household which provides labour to the firm and purchases sugar.The model explores the evolutionary dynamics whereby the firm does not initially know the household demand but eventually this demand and thus the correct price for sugar given the household’s optimal labour.
The model can be run in one of two ways; the first does not include money and the second uses money such that the firm and/or the household have an endowment that can be spent or saved. In either case, the household has preferences for leisure and consumption and a demand function relating sugar and price, and the firm has a production function and learns the household demand over a set number of time steps using either an endogenous or exogenous learning algorithm. The resulting equilibria, or fixed points of the system, may or may not match the classical economic equilibrium.
Exploring social psychology theory for modelling farmer decision-making
James Millington | Published Tuesday, September 18, 2012 | Last modified Saturday, April 27, 2013To investigate the potential of using Social Psychology Theory in ABMs of natural resource use and show proof of concept, we present an exemplary agent-based modelling framework that explicitly represents multiple and hierarchical agent self-concepts
Replication of ECEC model: Environmental Feedback and the Evolution of Cooperation
Pierre Bommel | Published Tuesday, April 05, 2011 | Last modified Saturday, April 27, 2013The model, presented here, is a re-implementation of the Pepper and Smuts’ model : - Pepper, J.W. and B.B. Smuts. 2000. “The evolution of cooperation in an ecological context: an agent-based model”. Pp. 45-76 in T.A. Kohler and G.J. Gumerman, eds. Dynamics of human and primate societies: agent-based modeling of social and spatial processes. Oxford University Press, Oxford. - Pepper, J.W. and B.B. Smuts. 2002. “Assortment through Environmental Feedback”. American Naturalist, 160: 205-213 […]
MERCURY extension: population
Tom Brughmans | Published Thursday, May 23, 2019This model is an extended version of the original MERCURY model (https://www.comses.net/codebases/4347/releases/1.1.0/ ) . It allows for experiments to be performed in which empirically informed population sizes of sites are included, that allow for the scaling of the number of tableware traders with the population of settlements, and for hypothesised production centres of four tablewares to be used in experiments.
Experiments performed with this population extension and substantive interpretations derived from them are published in:
Hanson, J.W. & T. Brughmans. In press. Settlement scale and economic networks in the Roman Empire, in T. Brughmans & A.I. Wilson (ed.) Simulating Roman Economies. Theories, Methods and Computational Models. Oxford: Oxford University Press.
…
Displaying 10 of 183 results for "J Gary Polhill" clear search