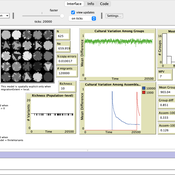
This structured population model is built to address how migration (or intergroup cultural transmission), copying error, and time-averaging affect regional variation in a single selectively neutral discrete cultural trait under different mechanisms of cultural transmission. The model allows one to quantify cultural differentiation between groups within a structured population (at equilibrium) as well as between regional assemblages of time-averaged archaeological material at two different temporal scales (1,000 and 10,000 ticks). The archaeological assemblages begin to accumulate only after a “burn-in” period of 10,000 ticks. The model includes two different representations of copying error: the infinite variants model of copying error and the finite model of copying error. The model also allows the user to set the variant ceiling value for the trait in the case of the finite model of copying error.

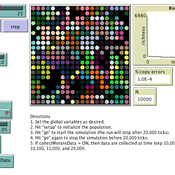
This model is designed to address the following research question: How does the amount and topology of intergroup cultural transmission modulate the effect of local group extinction on selectively neutral cultural diversity in a geographically structured population? The experimental design varies group extinction rate, the amount of intergroup cultural transmission, and the topology of intergroup cultural transmission while measuring the effects of local group extinction on long-term cultural change and regional cultural differentiation in a constant-size, spatially structured population. The results show that for most of the intergroup social network topologies tested here, increasing the amount of intergroup cultural transmission (similar to increasing gene flow in a genetic model) erases the negative effect of local group extinction on selectively neutral cultural diversity. The stochastic (i.e., preference attachment) network seems to stand out as an exception.

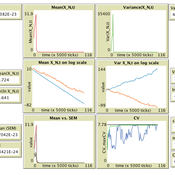
This version of the accumulated copying error (ACE) model is designed to address the following research question: how does finite population size (N) affect the coefficient of variation (CV) of a continuous cultural trait under the assumptions that the only source of copying error is visual perception error and that the continuous trait can take any positive value (i.e., it has no upper bound)? The model allows one to address this question while assuming the continuous trait is transmitted via vertical transmission, unbiased transmission, prestige biased transmission, mean conformist transmission, or median conformist transmission. By varying the parameter, p, one can also investigate the effect of population size under a mix of vertical and non-vertical transmission, whereby on average (1-p)N individuals learn via vertical transmission and pN individuals learn via either unbiased transmission, prestige biased transmission, mean conformist transmission, or median conformist transmission.

Previous work with the spatial iterated prisoner’s dilemma has shown that “walk away” cooperators are able to outcompete defectors as well as cooperators that do not respond to defection, but it remains to be seen just how robust the so-called walk away strategy is to ecologically important variables such as population density, error, and offspring dispersal. Our simulation experiments identify socio-ecological conditions in which natural selection favors strategies that emphasize forgiveness over flight in the spatial iterated prisoner’s dilemma. Our interesting results are best explained by considering how population density, error, and offspring dispersal affect the opportunity cost associated with walking away from an error-prone partner.

We employ this spatially explicit agent-based model to begin to examine how time-averaging can affect the spatial scale of cultural similarity in archaeological assemblage data. The model was built to address this question: to what extent does time-averaging affect the scale of local spatial association in the relative frequency of the most prevalent cultural variant in an archaeological landscape?

This model illustrates how the effective population size and the rate of change in mean skill level of a cultural trait are affected by the presence of natural selection and/or the cultural transmission mechanism by which it is passed.

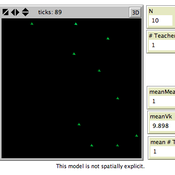
This spatially explicit agent-based model addresses how effective foraging radius (r_e) affects the effective size–and thus the equilibrium cultural diversity–of a structured population composed of central-place foraging groups.

This is a relatively simple foraging-radius model, as described first by Robert Kelly, that allows one to quantify the effect of increased logistical mobility (as represented by increased effective foraging radius, r_e) on the likelihood that 2 randomly placed central place foragers will encounter one another within 5000 time steps.