This is a re-implementation of a the NetLogo model Maze (ROOP, 2006).

This re-implementation makes use of the Q-Learning NetLogo Extension to implement the Q-Learning, which is done only with NetLogo native code in the original implementation.

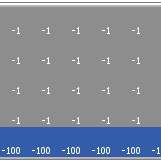
This model implements a classic scenario used in Reinforcement Learning problem, the “Cliff Walking Problem”. Consider the gridworld shown below (SUTTON; BARTO, 2018). This is a standard undiscounted, episodic task, with start and goal states, and the usual actions causing movement up, down, right, and left. Reward is -1 on all transitions except those into the region marked “The Cliff.” Stepping into this region incurs a reward of -100 and sends the agent instantly back to the start (SUTTON; BARTO, 2018).

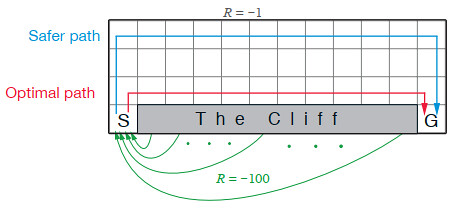
The problem is solved in this model using the Q-Learning algorithm. The algorithm is implemented with the support of the NetLogo Q-Learning Extension

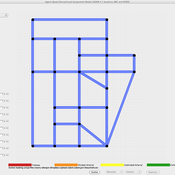
This is a generic sub-model of animal territory formation. It is meant to be a reusable building block, but not in the plug-and-play sense, as amendments are likely to be needed depending on the species and region. The sub-model comprises a grid of cells, reprenting the landscape. Each cell has a “quality” value, which quantifies the amount of resources provided for a territory owner, for example a tiger. “Quality” could be prey density, shelter, or just space. Animals are located randomly in the landscape and add grid cells to their intial cell until the sum of the quality of all their cells meets their needs. If a potential new cell to be added is owned by another animal, competition takes place. The quality values are static, and the model does not include demography, i.e. mortality, mating, reproduction. Also, movement within a territory is not represented.

Package for simulating the behavior of experts in a scientific-forecasting competition, where the outcome of experiments itself depends on expert consensus. We pay special attention to the interplay between expert bias and trust in the reward algorithm. The package allows the user to reproduce results presented in arXiv:2305.04814, as well as testing of other different scenarios.

A Repast Simphony model of interactions (conflict and cooperation) between states

The core algorithm is an agent-based model, which simulates travel patterns on a network based on microscopic decision-making by each traveler.

This spatially explicit agent-based model addresses how effective foraging radius (r_e) affects the effective size–and thus the equilibrium cultural diversity–of a structured population composed of central-place foraging groups.

This model can be used to explore under which conditions agents behave as observed in field experiments on irrigation games.

MELBIS-V1 is a spatially explicit agent-based model that allows the geospatial simulation of the decision-making process of newcomers arriving in the bilingual cities and boroughs of the island of Montreal, Quebec in CANADA, and the resulting urban segregation spatial patterns. The model was implemented in NetLogo, using geospatial raster datasets of 120m spatial resolution.

MELBIS-V2 enhances MELBIS-V1 to implement and simulate the decision-making processes of incoming immigrants, and to analyze the resulting spatial patterns of segregation as immigrants arrive and settle in various cities in Canada. The arrival and segregation of immigrants is modeled with MELBIS-V2 and compared for three major Canadian immigration gateways, including the City of Toronto, Metro Vancouver, and the City of Calgary.

The model simulates flood damages and its propagation through a cooperative, productive, farming system, characterized as a star-type network, where all elements in the system are connected one to each other through a central element.