Scholars have written extensively about hierarchical international order, on the one hand, and war on the other, but surprisingly little work systematically explores the connection between the two. This disconnect is all the more striking given that empirical studies have found a strong relationship between the two. We provide a generative computational network model that explains hierarchy and war as two elements of a larger recursive process: The threat of war drives the formation of hierarchy, which in turn shapes states’ incentives for war. Grounded in canonical theories of hierarchy and war, the model explains an array of known regularities about hierarchical order and conflict. Surprisingly, we also find that many traditional results of the IR literature—including institutional persistence, balancing behavior, and systemic self-regulation—emerge from the interplay between hierarchy and war.

This model describes and analyses the outcomes of the confrontation of interests, some conflicting, some common, about the management of a small river in SW France

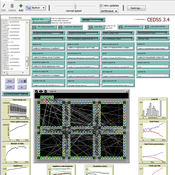
CEDSS is an agent-based model of domestic energy demand at the level of a small community.

Is the mass shooter a maniac or a relatively normal person in a state of great stress? According to the FBI report (Silver, J., Simons, A., & Craun, S. (2018). A Study of the Pre-Attack Behaviors of Active Shooters in the United States Between 2000 – 2013. Federal Bureau of Investigation, U.S. Department of Justice,Washington, D.C. 20535.), only 25% of the active shooters were known to have been diagnosed by a mental health professional with a mental illness of any kind prior to the offense.
The main objects of the model are the humans and the guns. The main factors influencing behavior are the population size, the number of people with mental disabilities (“psycho” in the model terminology) per 100,000 population, the total number of weapons (“guns”) in the population, the availability of guns for humans, the intensity of stressors affecting humans and the threshold level of stress, upon reaching which a person commits an act of mass shooting.
The key difference (in the model) between a normal person and a psycho is that a psycho accumulates stressors and, upon reaching a threshold level, commits an act of mass shooting. A normal person is exposed to stressors, but reaching the threshold level for killing occurs only when the simultaneous effect of stressors on him exceeds this level.
The population dynamics are determined by the following factors: average (normally distributed) life expectancy (“life_span” attribute of humans) and population growth with the percentage of newborns set by the value of the TickReprRatio% slider of the current population volume from 16 to 45 years old.Thus, one step of model time corresponds to a year.

The model presented here is extensively described in the paper ‘Talk less to strangers: How homophily can improve collective decision-making in diverse teams’ (forthcoming at JASSS). A full replication package reproducing all results presented in the paper is accessible at https://osf.io/76hfm/.

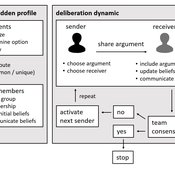
Narrative documentation includes a detailed description of the model, including a schematic figure and an extensive representation of the model in pseudocode.

The model develops a formal representation of a diverse work team facing a decision problem as implemented in the experimental setup of the hidden-profile paradigm. We implement a setup where a group seeks to identify the best out of a set of possible decision options. Individuals are equipped with different pieces of information that need to be combined to identify the best option. To this end, we assume a team of N agents. Each agent belongs to one of M groups where each group consists of agents who share a common identity.
The virtual teams in our model face a decision problem, in that the best option out of a set of J discrete options needs to be identified. Every team member forms her own belief about which decision option is best but is open to influence by other team members. Influence is implemented as a sequence of communication events. Agents choose an interaction partner according to homophily h and take turns in sharing an argument with an interaction partner. Every time an argument is emitted, the recipient updates her beliefs and tells her team what option she currently believes to be best. This influence process continues until all agents prefer the same option. This option is the team’s decision.

A model to show the effects of flood risk on a housing market; the role of flood protection for risk reduction; the working of the existing public-private flood insurance partnership in the UK, and the proposed scheme ‘Flood Re’.

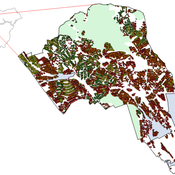
This model extends the original Artifical Anasazi (AA) model to include individual agents, who vary in age and sex, and are aggregated into households. This allows more realistic simulations of population dynamics within the Long House Valley of Arizona from AD 800 to 1350 than are possible in the original model. The parts of this model that are directly derived from the AA model are based on Janssen’s 1999 Netlogo implementation of the model; the code for all extensions and adaptations in the model described here (the Artificial Long House Valley (ALHV) model) have been written by the authors. The AA model included only ideal and homogeneous “individuals” who do not participate in the population processes (e.g., birth and death)–these processes were assumed to act on entire households only. The ALHV model incorporates actual individual agents and all demographic processes affect these individuals. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. Thus, the ALHV model is a combination of individual processes (birth and death) and household-level processes (e.g., finding suitable agriculture plots).

As is the case for the AA model, the ALHV model makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original model (from Janssen’s Netlogo implementation) to estimate annual maize productivity of various agricultural zones within the valley. These estimates are used to determine suitable locations for households and farms during each year of the simulation.

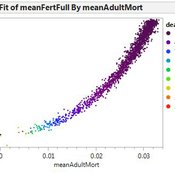
This model is an extension of the Artificial Long House Valley (ALHV) model developed by the authors (Swedlund et al. 2016; Warren and Sattenspiel 2020). The ALHV model simulates the population dynamics of individuals within the Long House Valley of Arizona from AD 800 to 1350. Individuals are aggregated into households that participate in annual agricultural and demographic cycles. The present version of the model incorporates features of the ALHV model including realistic age-specific fertility and mortality and, in addition, it adds the Black Mesa environment and population, as well as additional methods to allow migration between the two regions.

As is the case for previous versions of the ALHV model as well as the Artificial Anasazi (AA) model from which the ALHV model was derived (Axtell et al. 2002; Janssen 2009), this version makes use of detailed archaeological and paleoenvironmental data from the Long House Valley and the adjacent areas in Arizona. It also uses the same methods as the original AA model to estimate annual maize productivity of various agricultural zones within the Long House Valley. A new environment and associated methods have been developed for Black Mesa. Productivity estimates from both regions are used to determine suitable locations for households and farms during each year of the simulation.

ForagerNet3_Demography is a non-spatial ABM for exploring hunter-gatherer demography. Key methods represent birth, death, and marriage. The dependency ratio is an imporant variable in many economic decisions embedded in the methods.

ForagerNet3_Demography_V2 is a non-spatial ABM for exploring hunter-gatherer demography. This version (developed from FN3D_V1) contains code for calculating the ratio of old to young adults (the “OY ratio”) in the living and dead populations.