About the CoMSES Model Library more info
Our mission is to help computational modelers at all levels engage in the establishment and adoption of community standards and good practices for developing and sharing computational models. Model authors can freely publish their model source code in the Computational Model Library alongside narrative documentation, open science metadata, and other emerging open science norms that facilitate software citation, reproducibility, interoperability, and reuse. Model authors can also request peer review of their computational models to receive a DOI.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with additional detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 951 results for "Chantal van Esch" clear search
Peer reviewed Personnel decisions in the hierarchy
Smarzhevskiy Ivan | Published Friday, August 19, 2022This is a model of organizational behavior in the hierarchy in which personnel decisions are made.
The idea of the model is that the hierarchy, busy with operations, is described by such characteristics as structure (number and interrelation of positions) and material, filling these positions (persons with their individual performance). A particular hierarchy is under certain external pressure (performance level requirement) and is characterized by the internal state of the material (the distribution of the perceptions of others over the ensemble of persons).
The World of the model is a four-level hierarchical structure, consisting of shuff positions of the top manager (zero level of the hierarchy), first-level managers who are subordinate to the top manager, second-level managers (subordinate to the first-level managers) and positions of employees (the third level of the hierarchy). ) subordinated to the second-level managers. Such a hierarchy is a tree, i.e. each position, with the exception of the position of top manager, has a single boss.
Agents in the model are persons occupying the specified positions, the number of persons is set by the slider (HumansQty). Personas have some operational performance (harisma, an unfortunate attribute name left over from the first edition of the model)) and a sense of other personas’ own perceptions. Performance values are distributed over the ensemble of persons according to the normal law with some mean value and variance.
The value of perception by agents of each other is positive or negative (implemented in the model as numerical values equal to +1 and -1). The distribution of perceptions over an ensemble of persons is implemented as a random variable specified by the probability of negative perception, the value of which is set by the control elements of the model interface. The numerical value of the probability equal to 0 corresponds to the case in which all persons positively perceive each other (the numerical value of the random variable is equal to 1, which corresponds to the positive perception of the other person by the individual).
The hierarchy is occupied with operational activity, the degree of intensity of which is set by the external parameter Difficulty. The level of productivity of each manager OAIndex is equal to the level of productivity of the department he leads and is the ratio of the sum of productivity of employees subordinate to the head to the level of complexity of the work Difficulty. An increase in the numerical value of Difficulty leads to a decrease in the OAIndex for all subdivisions of the hierarchy. The managerial meaning of the OAIndex indicator is the percentage of completion of the load specified for the hierarchy as a whole, i.e. the ratio of the actual performance of the structural subdivisions of the hierarchy to the required performance, the level of which is specified by the value of the Difficulty parameter.
…
Diffusion dynamics in small-world networks with heterogeneous consumers
Sebastiano Delre | Published Saturday, September 10, 2011 | Last modified Saturday, April 27, 2013This model simulates diffusion curves and it allows to test how social influence, network structure and consumer heterogeneity affect their spreads and their speeds.
03 MppLab V1.09 – Maximum Power Principle Laboratory
Garvin Boyle | Published Saturday, April 15, 2017Using webs of replicas of Atwood’s Machine, we explore implications of the Maximum Power Principle. This is one of a series of models exploring the dynamics of sustainable economics – PSoup, ModEco, EiLab, OamLab, MppLab, TpLab, CmLab.
Adoption as a social marker
Paul Smaldino | Published Monday, October 17, 2016A model of innovation diffusion in a structured population with two groups who are averse to adopting a produce popular with the outgroup.
AMMA: Agent-based Model of the Media Arena
Annie Waldherr | Published Tuesday, February 11, 2014The AMMA simulates how news waves emerge in the mass media. Drawing on the ideas of public arena models and issue-attention cycles, it represents fundamental principles of public communication in a virtual media system.
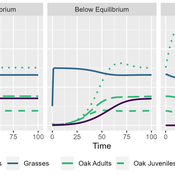
Peer reviewed Theoretical Model of Oak Persistence Under Competition and Herbivory
MV Eitzel Solera | Published Tuesday, October 25, 2022This model is intended to support oak tree management by representing the dynamics of oaks in multiple life stages and their competitors and consumers. This is implemented using a differential equation-based theoretical model representing three life stages of oaks: seedlings, juveniles, and adults. It includes the population dynamics of seedlings transitioning to juveniles, juveniles to adults, and adults producing new seedlings, as well as survival rates for each of the stages. It also includes a model of competition for light and water within seedlings and between seedlings and annual grasses. Finally, there is a predation term representing herbivores eating seedlings and grasses, using a Holling Type II (satiating) response with interference for predators and a death rate which depends on the resource extraction rate.
Peer reviewed Swidden Farming Version 2.0
C Michael Barton | Published Wednesday, June 12, 2013 | Last modified Wednesday, September 03, 2014Model of shifting cultivation. All parameters can be controlled by the user or the model can be run in adaptive mode, in which agents innovate and select parameters.
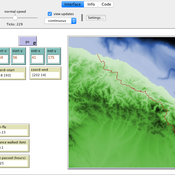
Peer reviewed Least cost path mobility
Colin Wren Claudine Gravel-Miguel | Published Saturday, September 02, 2017 | Last modified Monday, October 04, 2021This model aims to mimic human movement on a realistic topographical surface. The agent does not have a perfect knowledge of the whole surface, but rather evaluates the best path locally, at each step, thus mimicking imperfect human behavior.
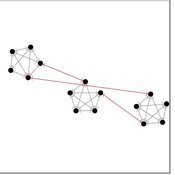
The influence of cognitive diversity on networked search and coordination
César García-Díaz | Published Wednesday, April 03, 2024Agent-based models of organizational search have long investigated how exploitative and exploratory behaviors shape and affect performance on complex landscapes. To explore this further, we build a series of models where agents have different levels of expertise and cognitive capabilities, so they must rely on each other’s knowledge to navigate the landscape. Model A investigates performance results for efficient and inefficient networks. Building on Model B, it adds individual-level cognitive diversity and interaction based on knowledge similarity. Model C then explores the performance implications of coordination spaces. Results show that totally connected networks outperform both hierarchical and clustered network structures when there are clear signals to detect neighbor performance. However, this pattern is reversed when agents must rely on experiential search and follow a path-dependent exploration pattern.
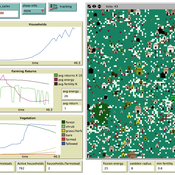
Critical Sustainability Transitions: Relaunching local agriculture after decline (Model code and description)
Pedro Lopez-Merino | Published Tuesday, April 30, 2024This model simulates the dynamics of agricultural land use change, specifically the transition between agricultural and non-agricultural land use in a spatial context. It explores the influence of various factors such as agricultural profitability, path dependency, and neighborhood effects on land use decisions.
The model operates on a grid of patches representing land parcels. Each patch can be in one of two states: exploited (green, representing agricultural land) or unexploited (brown, representing non-agricultural land). Agents (patches) transition between these states based on probabilistic rules. The main factors affecting these transitions are agricultural profitability, path dependency, and neighborhood effects.
-Agricultural Profitability: This factor is determined by the prob-agri function, which calculates the probability of a non-agricultural patch converting to agricultural based on income differences between agriculture and other sectors. -Path Dependency: Represented by the path-dependency parameter, it influences the likelihood of patches changing their state based on their current state. It’s a measure of inertia or resistance to change. -Neighborhood Effects: The neighborhood function calculates the number of exploited (agricultural) neighbors of a patch. This influences the decision of a patch to convert to agricultural land, representing the influence of surrounding land use on the decision-making process.
Displaying 10 of 951 results for "Chantal van Esch" clear search