About the CoMSES Model Library more info
Our mission is to help computational modelers at all levels engage in the establishment and adoption of community standards and good practices for developing and sharing computational models. Model authors can freely publish their model source code in the Computational Model Library alongside narrative documentation, open science metadata, and other emerging open science norms that facilitate software citation, reproducibility, interoperability, and reuse. Model authors can also request peer review of their computational models to receive a DOI.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with additional detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 250 results for "Hans-Joerg Althaus" clear search
ABM for Underwater optical wireless communication in a water tank
Mohamed ABID | Published Sunday, May 29, 2022This model simulates the propagation of photons in a water tank. A source of light emits an impulse of photons with equal energy represented by yellow dots. These photons are then scattered by water particles before possibly reaching the photo-detector represented by a gray line. Different types of water are considered. For each one of them we calculate the total received energy.
The water tank is represented by a blue rectangle with fixed dimensions. It’s exposed to the air interface and has totally absorbent barriers. Four types of water are supported. Each one is characterized by its absorption and scattering coefficients.
At the source, the photons are generated uniformly with a random direction within the beamwidth. Each photon travels a random distance drawn from a distribution depending on the water characteristics before encountering a water particle.
Based on the updated position of the photon, three situations may occur:
-The photon hits the barrier of the tank on its trajectory. In this case it’s considered as lost since the barriers are assumed totally absorbent.
…
Exploring the Potential of Conversational AI Support for Agent-Based Social Simulation Model Design
Peer-Olaf Siebers | Published Sunday, May 12, 2024Our aim is to demonstrate how conversational AI systems, exemplified by ChatGPT, can support the conceptualisation of Agent-Based Social Simulation (ABSS) models, leading to a full ABSS model design document. Through advanced prompt engineering and adherence to the Engineering ABSS framework (Siebers and Klügl 2017), we have constructed a comprehensive script that is easy to use and that supports the design of ABSS models with or even by AI. The performance of the script is demonstrated through an illustrative case study related to the use of adaptive architecture in museums. The repository contains (1) the comprehensive script in a format that allows copying and pasting prompts for use with ChatGPT, (2) the results of the illustrative case study in the form of two conceptual ABSS models, the ground truth and the autogenerated version.
On July 20th, James Holmes committed a mass shooting in a midnight showing of The Dark Knight Rises. The Aurora Colorado shooting was used as a test case to validate this framework for modeling mass shootings.
06b EiLab_Model_I_V5.00 NL
Garvin Boyle | Published Saturday, October 05, 2019EiLab - Model I - is a capital exchange model. That is a type of economic model used to study the dynamics of modern money which, strangely, is very similar to the dynamics of energetic systems. It is a variation on the BDY models first described in the paper by Dragulescu and Yakovenko, published in 2000, entitled “Statistical Mechanics of Money”. This model demonstrates the ability of capital exchange models to produce a distribution of wealth that does not have a preponderance of poor agents and a small number of exceedingly wealthy agents.
This is a re-implementation of a model first built in the C++ application called Entropic Index Laboratory, or EiLab. The first eight models in that application were labeled A through H, and are the BDY models. The BDY models all have a single constraint - a limit on how poor agents can be. That is to say that the wealth distribution is bounded on the left. This ninth model is a variation on the BDY models that has an added constraint that limits how wealthy an agent can be? It is bounded on both the left and right.
EiLab demonstrates the inevitable role of entropy in such capital exchange models, and can be used to examine the connections between changing entropy and changes in wealth distributions at a very minute level.
…
An agent-based model of school enrollment process under educational competition
Yao Tong | Published Sunday, August 04, 2024Due to the role of education in promoting social status and facilitating upward social mobility, individuals and their families spare no effort to pursue better educational opportunities, especially in countries where education is highly competitive.
In China, the enrollment of senior high schools and universities mainly follows a ranking system based on students’ scores in national entrance exams (Zhongkao and Gaokao). Typically, students with higher scores have priority in choosing schools and endeavor to get into better senior high schools to increase their chances of entering a prestigious university.
However, students can only select “better” senior high schools based on their average Gaokao grades, which are strongly influenced by the initial performance (Zhongkao grades) of enrolled students. The true quality indicator of school education (schooling effect, defined as the grade improvement achieved through education at the senior high school) is unknowable. This raises the first question: will school rankings reflect the real educational quality of schools over decades of educational competition, or merely the initial quality of the students they enroll?
…
Digital divide and opinion formation
Dongwon Lim | Published Friday, November 02, 2012 | Last modified Monday, May 20, 2013This model extends the bounded confidence model of Deffuant and Weisbuch. It introduces online contexts in which a person can deliver his or her opinion to several other persons. There are 2 additional parameters accessibility and connectivity.
Soy2Grow-ABM-V1
Siavash Farahbakhsh | Published Monday, January 20, 2025The Soy2Grow ABM aims to simulate the adoption of soybean production in Flanders, Belgium. The model primarily considers two types of agents as farmers: 1) arable and 2) dairy farmers. Each farmer, based on its type, assesses the feasibility of adopting soybean cultivation. The feasibility assessment depends on many interrelated factors, including price, production costs, yield, disease, drought (i.e., environmental stress), social pressure, group formations, learning and skills, risk-taking, subsidies, target profit margins, tolerance to bad experiences, etc. Moreover, after adopting soybean production, agents will reassess their performance. If their performance is unsatisfactory, an agent may opt out of soy production. Therefore, one of the main outcomes to look for in the model is the number of adopters over time.
The main agents are farmers. Generally, factors influencing farmers’ decision-making are divided into seven main areas: 1) external environmental factors, 2) cooperation and learning (with slight differences depending on whether they are arable or dairy farmers), 3) crop-specific factors, 4) economics, 5) support frameworks, 6) behavioral factors, and 7) the role of mobile toasters (applicable only to dairy farmers).
Moreover, factors not only influence decision-making but also interact with each other. Specifically, external environmental factors (i.e., stress) will result in lower yield and quality (protein content). The reducing effect, identified during participatory workshops, can reach 50 %. Skills can grow and improve yield; however, their growth has a limit and follows different learning curves depending on how individualistic a farmer is. During participatory workshops, it was identified that, contrary to cooperative farmers, individualistic farmers may learn faster and reach their limits more quickly. Furthermore, subsidies directly affect revenues and profit margins; however, their impact may disappear when they are removed. In the case of dairy farmers, mobile toasters play an important role, adding toasting and processing costs to those producing soy for their animal feed consumption.
Last but not least, behavioral factors directly influence the final adoption decision. For example, high risk-taking farmers may adopt faster, whereas more conservative farmers may wait for their neighbors to adopt first. Farmers may evaluate their success based on their own targets and may also consider other crops rather than soy.
Exploring social psychology theory for modelling farmer decision-making
James Millington | Published Tuesday, September 18, 2012 | Last modified Saturday, April 27, 2013To investigate the potential of using Social Psychology Theory in ABMs of natural resource use and show proof of concept, we present an exemplary agent-based modelling framework that explicitly represents multiple and hierarchical agent self-concepts
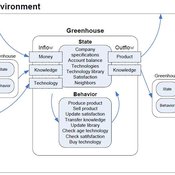
Universal Darwinism in Dutch Greenhouses
Julia Kasmire | Published Wednesday, May 09, 2012 | Last modified Saturday, April 27, 2013An ABM, derived from a case study and a series of surveys with greenhouse growers in the Westland, Netherlands. Experiments using this model showshow that the greenhouse horticulture industry displays diversity, adaptive complexity and an uneven distribution, which all suggest that the industry is an evolving system.
The Evolution of Multiple Resistant Strains: An Abstract Model of Systemic Treatment and Accumulated Resistance
Benjamin Nye | Published Wednesday, August 31, 2011 | Last modified Saturday, April 27, 2013This model is intended to explore the effectiveness of different courses of interventions on an abstract population of infections. Illustrative findings highlight the importance of the mechanisms for variability and mutation on the effectiveness of different interventions.
Displaying 10 of 250 results for "Hans-Joerg Althaus" clear search