About the CoMSES Model Library more info
Our mission is to help computational modelers at all levels engage in the establishment and adoption of community standards and good practices for developing and sharing computational models. Model authors can freely publish their model source code in the Computational Model Library alongside narrative documentation, open science metadata, and other emerging open science norms that facilitate software citation, reproducibility, interoperability, and reuse. Model authors can also request peer review of their computational models to receive a DOI.
All users of models published in the library must cite model authors when they use and benefit from their code.
Please check out our model publishing tutorial and contact us if you have any questions or concerns about publishing your model(s) in the Computational Model Library.
We also maintain a curated database of over 7500 publications of agent-based and individual based models with additional detailed metadata on availability of code and bibliometric information on the landscape of ABM/IBM publications that we welcome you to explore.
Displaying 10 of 257 results for "Philipp S. Sommer" clear search
An age and/or gender-based division of labor during the Last Glacial Maximum in Iberia through rabbit hunting
Liliana Perez Samuel Seuru Ariane Burke | Published Thursday, February 29, 2024Many archaeological assemblages from the Iberian Peninsula dated to the Last Glacial Maximum contain large quantities of European rabbit (Oryctolagus cuniculus) remains with an anthropic origin. Ethnographic and historic studies report that rabbits may be mass-collected through warren-based harvesting involving the collaborative participation of several persons.
We propose and implement an Agent-Based Model grounded in the Optimal Foraging Theory and the Diet Breadth Model to examine how different warren-based hunting strategies influence the resulting human diets.
…
Spatial model of the noisy Prisoner's Dilemma with reward shift
Matus Halas | Published Thursday, March 05, 2015 | Last modified Tuesday, May 29, 2018Interactions of players embedded in a closed square lattice are determined by distance and overall gains and they lead to shifts of reward payoff between temptation and punishment. A new winner balancing against threats is ultimately discovered.
Peer reviewed Zimbabwe Agro-Pastoral Management Model (ZAPMM): Musimboti wevanhu, zvipfuo nezvirimwa
MV Eitzel Solera Kleber Tulio Neves Jon Solera Kenneth B Wilson Abraham Mawere Ndlovu Aaron C Fisher André Veski Oluwasola E Omoju Emmanuel Mhike Hove | Published Tuesday, June 19, 2018This model has been created with and for the researcher-farmers of the Muonde Trust (http://www.muonde.org/), a registered Zimbabwean non-governmental organization dedicated to fostering indigenous innovation. Model behaviors and parameters (mashandiro nemisiyano nedzimwe model) derive from a combination of literature review and the collected datasets from Muonde’s long-term (over 30 years) community-based research. The goals of this model are three-fold (muzvikamu zvitatu):
A) To represent three components of a Zimbabwean agro-pastoral system (crops, woodland grazing area, and livestock) along with their key interactions and feedbacks and some of the human management decisions that may affect these components and their interactions.
B) To assess how climate variation (implemented in several different ways) and human management may affect the sustainability of the system as measured by the continued provisioning of crops, livestock, and woodland grazing area.
C) To provide a discussion tool for the community and local leaders to explore different management strategies for the agro-pastoral system (hwaro/nzira yekudyidzana kwavanhu, zvipfuo nezvirimwa), particularly in the face of climate change.
Peer reviewed BAMERS: Macroeconomic effect of extortion
Alejandro Platas López Alejandro Guerra-Hernández | Published Monday, March 23, 2020 | Last modified Sunday, July 26, 2020Inspired by the European project called GLODERS that thoroughly analyzed the dynamics of extortive systems, Bottom-up Adaptive Macroeconomics with Extortion (BAMERS) is a model to study the effect of extortion on macroeconomic aggregates through simulation. This methodology is adequate to cope with the scarce data associated to the hidden nature of extortion, which difficults analytical approaches. As a first approximation, a generic economy with healthy macroeconomics signals is modeled and validated, i.e., moderate inflation, as well as a reasonable unemployment rate are warranteed. Such economy is used to study the effect of extortion in such signals. It is worth mentioning that, as far as is known, there is no work that analyzes the effects of extortion on macroeconomic indicators from an agent-based perspective. Our results show that there is significant effects on some macroeconomics indicators, in particular, propensity to consume has a direct linear relationship with extortion, indicating that people become poorer, which impacts both the Gini Index and inflation. The GDP shows a marked contraction with the slightest presence of extortion in the economic system.
While the world’s total urban population continues to grow, not all cities are witnessing such growth, some are actually shrinking. This shrinkage causes several problems to emerge including population loss, economic depression, vacant properties and the contraction of housing markets. Such problems challenge efforts to make cities sustainable. While there is a growing body of work on study shrinking cities, few explore such a phenomenon from the bottom up using dynamic computational models. To overcome this issue this paper presents an spatially explicit agent-based model stylized on the Detroit Tri-county area, an area witnessing shrinkage. Specifically, the model demonstrates how through the buying and selling of houses can lead to urban shrinkage from the bottom up. The model results indicate that along with the lower level housing transactions being captured, the aggregated level market conditions relating to urban shrinkage are also captured (i.e., the contraction of housing markets). As such, the paper demonstrates the potential of simulation to explore urban shrinkage and potentially offers a means to test polices to achieve urban sustainability.
Hybrid agent-based methodology for testing response protocols
Fernando Sancho Caparrini | Published Wednesday, February 03, 2021In recent years we have seen multiple incidents with a large number of people injured and killed by one or more armed attackers. Since this type of violence is difficult to predict, detecting threats as early as possible allows to generate early warnings and reduce response time. In this context, any tool to check and compare different action protocols can be a further step in the direction of saving lives. Our proposal combines features from continuous and discrete models to obtain the best of both worlds in order to simulate large and crowded spaces where complex behavior individuals interact. With this proposal we aim to provide a tool for testing different security protocols under several emergency scenarios, where spaces, hazards, and population can be customized. Finally, we use a proof of concept implementation of this model to test specific security protocols under emergency situations for real spaces. Specifically, we test how providing some users of a university college with an app that informs about the type and characteristics of the ongoing hazard, affects in the safety performance.
Simulation model replicating the five different games that were run during a workshop of the TISSS Lab
tissslab | Published Friday, April 30, 2021The three-day participatory workshop organized by the TISSS Lab had 20 participants who were academics in different career stages ranging from university student to professor. For each of the five games, the participants had to move between tables according to some pre-specified rules. After the workshop both the participant’s perception of the games’ complexities and the participants’ satisfaction with the games were recorded.
In order to obtain additional objective measures for the games’ complexities, these games were also simulated using this simulation model here. Therefore, the simulation model is an as-accurate-as-possible reproduction of the workshop games: it has 20 participants moving between 5 different tables. The rules that specify who moves when vary from game to game. Just to get an idea, Game 3 has the rule: “move if you’re sitting next to someone who is waring white or no socks”.
An exact description of the workshop games and the associated simulation models can be found in the paper “The relation between perceived complexity and happiness with decision situations: searching for objective measures in social simulation games”.
Simulating the cost of social care in an ageing population
Eric Silverman | Published Thursday, September 16, 2021This model is an agent-based simulation written in Python 2.7, which simulates the cost of social care in an ageing UK population. The simulation incorporates processes of population change which affect the demand for and supply of social care, including health status, partnership formation, fertility and mortality. Fertility and mortality rates are drawn from UK population data, then projected forward to 2050 using the methods developed by Lee and Carter 1992.
The model demonstrates that rising life expectancy combined with lower birthrates leads to growing social care costs across the population. More surprisingly, the model shows that the oft-proposed intervention of raising the retirement age has limited utility; some reductions in costs are attained initially, but these reductions taper off beyond age 70. Subsequent work has enhanced and extended this model by adding more detail to agent behaviours and familial relationships.
The version of the model provided here produces outputs in a format compatible with the GEM-SA uncertainty quantification software by Kennedy and O’Hagan. This allows sensitivity analyses to be performed using Gaussian Process Emulation.
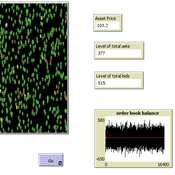
Peer reviewed A financial market with zero intelligence agents
edgarkp | Published Wednesday, March 27, 2024The model’s aim is to represent the price dynamics under very simple market conditions, given the values adopted by the user for the model parameters. We suppose the market of a financial asset contains agents on the hypothesis they have zero-intelligence. In each period, a certain amount of agents are randomly selected to participate to the market. Each of these agents decides, in a equiprobable way, between proposing to make a transaction (talk = 1) or not (talk = 0). Again in an equiprobable way, each participating agent decides to speak on the supply (ask) or the demand side (bid) of the market, and proposes a volume of assets, where this number is drawn randomly from a uniform distribution. The granularity depends on various factors, including market conventions, the type of assets or goods being traded, and regulatory requirements. In some markets, high granularity is essential to capture small price movements accurately, while in others, coarser granularity is sufficient due to the nature of the assets or goods being traded
Alpine land-use allocation model - ALUAM-AB
Simon Briner | Published Tuesday, January 31, 2012 | Last modified Saturday, April 27, 2013A model for simulating farmers and foresters response on changing climate and changing socio-economic parameters. Modeled are changes in land-use as well as in ecosystem services provision.
Displaying 10 of 257 results for "Philipp S. Sommer" clear search